Map projections transfer the spherical earth onto a two-dimensional surface. This process introduces errors. Depending on the projection method chosen, there might be a distortion in directions while distances are displayed accurately. Sometimes, shape may be preserved at the expense of accurate area estimates. Different map projections have been prepared for different parts of the world for mapping different sized areas and for different applications. There are hundreds of different map projections. The results of analysis will be affected in different ways by different map projections.
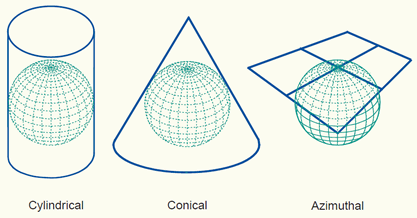
Depending on the development surface, map projections can be classified into:
Conic projection, Cylindrical projection and Planar or Azimuthal projection families as shown below.
One of the functions of a GIS is to allow the integration of data from different sources, the ability to ALTER projections is a fundamental ability of many GIS. There are hundreds of different map projections and some GIS provide the capability to reproject data for most of these.
SPATIAL REFERENCING
A referencing system is used to locate a feature on the Earth's surface (3 dimensional) or a map of the Earth (2 dimensional). Several methods of spatial referencing exist and they can be grouped into three categories listed below:
-Geographic Coordinate System (GCS)
-Rectangular Coordinate System (RCS) and
-Non-Coordinate System (NCS)
The only true GEOGRAPHIC COORDINATES are LATITUDE and LONGITUDE
Lines of longitude are also called MERIDIANS
The arbitrary choice for a central line of longitude is that which runs through the Royal Observatory in Greenwich, England. It is also called PRIME MERIDIAN.
The meridians are widest apart at the Equator and closest together at the Poles
The relative distance between lines of longitude where they intersect lines of latitude is ALWAYS EQUAL.
lines of latitude lie at right angles to lines of longitude and run parallel to one another
The latitude with the greatest circumference is called the EQUATOR (Central parallel) and it is equidistant from the poles.
At the poles, the lines of latitude are represented by a single point - the pole.
Using the lines of longitude and lines of latitude, ANY POINT ON THE EARTH's SURFACE can be loacated in degrees and minutes.
All features on the Earth can be located relative to one another and the distance between them can be calculated.
The shortest distance between TWO points on the Earths surface is known as GREAT CIRCLE DISTANCE.
Examples of RCS are:
-UK Ordnance Survey's National Grid and
-Universal Transverse Mercator (UTM) plane grid system
Non-Coordinate Systems provide spatial references using a descriptive code rather than a coordinate. Examples are postal codes used throughout the world. While some of the codes are fully numeric (U.S. post codes, Indian PIN codes), others are alphanumeric (U.K. post codes). The advantage of this system is that it is used by the postal department and hence continuously maintained and updated. In the wester
A Geographic Coordinate System (GCS) defines locations on the Earth using a three dimensional spherical surface. A GCS includes:
-An angular unit of measure
-A prime meridian and
-A datum (based on a spheroid)
The longitudes and latitudes encompass the globe forming a gridded network called a GRATICULE
The equator defines the line of ZERO latitude. The prime meridian defines the line of ZERO longitude. The point where the zero latitude and zero longitude intersect defines the origin (0,0)
Circles with the same radius as the spherical Earth are called GREAT CIRCLES. ALL MERIDIANS AND THE EQUATOR ARE GREAT CIRCLES.
Although the Earth is assumed to be roughly spherical for most practical considerations, with all its irregularities due to the various natural landforms, it is now a well accepted fact that the shape of the Earth is an OBLATE SPHEROID.
The Earth is sometimes assumed to be SPHERICAL to make mathematical calculations easier. For a small scale map (1:5,000,000) the difference between a sphere and a spheroid is not detectable. However, for large scale maps (1:1,000,000) a spheroid is necessary to accurately represent the of shape of the Earth.
A spheroid is defined by:
-semi-major axis 'a' or
-semi-minor axis 'b' or
-flattening
flattening (f) = (a-b)/a flattening is a small value; hence 1/f is generally used.
Flattening ranges between 0 and 1. Flattening of the Earth is approximately 0.003353
Square of the eccentricity is similar to flattening and describes the shape of a spheroid
e^2 = (a^2-b^2)/a^2
Depending on the development surface, map projections can be classified into:
Conic projection, Cylindrical projection and Planar or Azimuthal projection families as shown below.

One of the functions of a GIS is to allow the integration of data from different sources, the ability to ALTER projections is a fundamental ability of many GIS. There are hundreds of different map projections and some GIS provide the capability to reproject data for most of these.
SPATIAL REFERENCING
A referencing system is used to locate a feature on the Earth's surface (3 dimensional) or a map of the Earth (2 dimensional). Several methods of spatial referencing exist and they can be grouped into three categories listed below:
-Geographic Coordinate System (GCS)
-Rectangular Coordinate System (RCS) and
-Non-Coordinate System (NCS)
The only true GEOGRAPHIC COORDINATES are LATITUDE and LONGITUDE
Lines of longitude are also called MERIDIANS
The arbitrary choice for a central line of longitude is that which runs through the Royal Observatory in Greenwich, England. It is also called PRIME MERIDIAN.
The meridians are widest apart at the Equator and closest together at the Poles
The relative distance between lines of longitude where they intersect lines of latitude is ALWAYS EQUAL.
lines of latitude lie at right angles to lines of longitude and run parallel to one another
The latitude with the greatest circumference is called the EQUATOR (Central parallel) and it is equidistant from the poles.
At the poles, the lines of latitude are represented by a single point - the pole.
Using the lines of longitude and lines of latitude, ANY POINT ON THE EARTH's SURFACE can be loacated in degrees and minutes.
All features on the Earth can be located relative to one another and the distance between them can be calculated.
The shortest distance between TWO points on the Earths surface is known as GREAT CIRCLE DISTANCE.
Examples of RCS are:
-UK Ordnance Survey's National Grid and
-Universal Transverse Mercator (UTM) plane grid system
Non-Coordinate Systems provide spatial references using a descriptive code rather than a coordinate. Examples are postal codes used throughout the world. While some of the codes are fully numeric (U.S. post codes, Indian PIN codes), others are alphanumeric (U.K. post codes). The advantage of this system is that it is used by the postal department and hence continuously maintained and updated. In the wester
A Geographic Coordinate System (GCS) defines locations on the Earth using a three dimensional spherical surface. A GCS includes:
-An angular unit of measure
-A prime meridian and
-A datum (based on a spheroid)
The longitudes and latitudes encompass the globe forming a gridded network called a GRATICULE
The equator defines the line of ZERO latitude. The prime meridian defines the line of ZERO longitude. The point where the zero latitude and zero longitude intersect defines the origin (0,0)
Circles with the same radius as the spherical Earth are called GREAT CIRCLES. ALL MERIDIANS AND THE EQUATOR ARE GREAT CIRCLES.
Although the Earth is assumed to be roughly spherical for most practical considerations, with all its irregularities due to the various natural landforms, it is now a well accepted fact that the shape of the Earth is an OBLATE SPHEROID.
The Earth is sometimes assumed to be SPHERICAL to make mathematical calculations easier. For a small scale map (1:5,000,000) the difference between a sphere and a spheroid is not detectable. However, for large scale maps (1:1,000,000) a spheroid is necessary to accurately represent the of shape of the Earth.
A spheroid is defined by:
-semi-major axis 'a' or
-semi-minor axis 'b' or
-flattening
flattening (f) = (a-b)/a flattening is a small value; hence 1/f is generally used.
Flattening ranges between 0 and 1. Flattening of the Earth is approximately 0.003353
Square of the eccentricity is similar to flattening and describes the shape of a spheroid
e^2 = (a^2-b^2)/a^2
No comments:
Post a Comment